Endgame decomposer

Before I move on to the more complicated pawn endings with 3 pawns or more, I want to have a clear picture of all endgames with 2 pawns.
Since a position with 3 pawns can become a position with 2 pawns by saccing or conquering a pawn.

Why am I making such a big issue of this?
Yesterday I came across a study of TCT with Kpp vs Kp.
The author of TCT is of master level.
He made fun of the majority of people who would move the h-pawn in that position, which would result in a draw instead of a win.
He told that moving the g-pawn instead would be an easy win.
So I checked it with my Nalimov tablebase and that move was a draw too!
The only winning move was a counter intuitive king move he hadn't mentioned.

So if a master, who has spend hours at the preparation of a study position for his students, still makes such errors, these positions must not be underestimated!
Margriet and I couldn't find the logic behind the illogical-looking king move.
But it was clear that knowledge of the underlying 2-pawn positions was essential.
And thus I went back to the basics.

My previous post showed an easy looking yet complicated position with two pawns.
The tree of analysis of that position consists of 5 branches and 40+ leaves.
That is an enormous amount of calculation that has to be done if you encounter such positions in an OTB game.
I guess that a lot of people will dismiss this position by counting the material and say that this is a dead draw. And indeed, if both sides overlook the subtleties of the position, it maybe will proof to be a draw!

If such an easy position leads allready to so much calculation, how am I ever going to master this? That's why I decided to look after a method to prune the tree of analysis drastically.
I think I have found at least a part of this method.
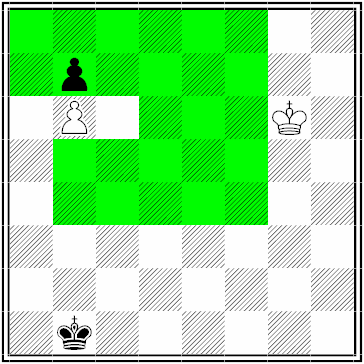
In my last post I showed you the following diagram.

diagram 1





















White to move and draw.
green = white wins
blue = draw
red = black wins

White has of course to move to the blue zone with 1.Kg3!!
How can these zones be determined in any given position of Kp vs Kp?
I did this with the help of my Nalimov endgame tablebase.
But since that isn't allowed in an OTB game, we have to find another method.
This is my try.

Let's have a look at the different underlying zones.
To begin with the green winning zone.

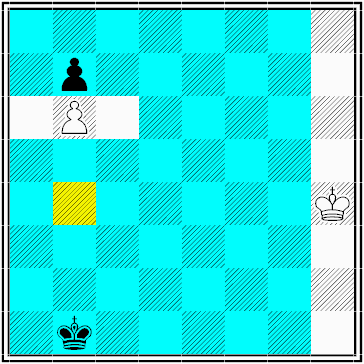
diagram 2





















White to move.

If white steps on a green square he will be in time to conquer the black pawn.
This is a position where I have neglected the interference between the white and the black king.
The geometry of the zone is quite determined by the distance between the white king and black pawn (5), compared with the distance between the black king and the white pawn (5)
Notice that the squares a3, a4, a5, b3 and c3 omit from the winning zone.
That's because I haven't taken the interference between the kings into account.
If I do take that into account, the white king will shoulder away the black king and these squares have to be added to the green zone.

Let's have a look at the underlying draw zone.
In this position I neglect the interference between the kings and I neglect the fact that white can win by conquering the black pawn.
The basis of the position is the keysquare b4.
If white reaches b4 at the moment the black king snacks the white pawn, white can hold the draw.

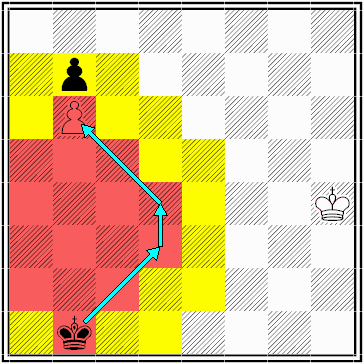
diagram 3





















White to move.
blue = draw zone
yellow = key square

The geometry of the position depends solely on the distance between the white king and the key square (6) and the distance between the black king and the white pawn (5)
The former (6) can be greater than the latter (5) because white starts to move, but the black king is allowed to reach b6 before the white king reaches b4, without disturbing the draw.

Now we have to look at a more complicated point, the interference of the kings.

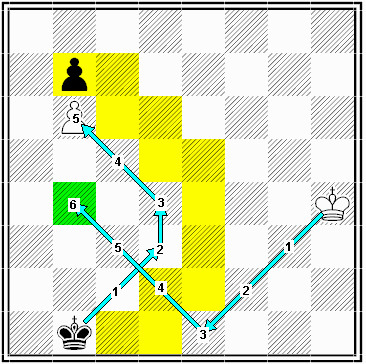
diagram 4





















red = shortest path of the black king to the white pawn (5 moves)
yellow = the "shoulder of the black king"

There are a lot of ways to get to the white pawn. All of them with a length of 5 moves. All of them go thru the red zone. The path that hinders the white king the most will be along the blue arrow. I call this the ideal path of the black king.
The white king has 141 methods to get to b5 in 6 moves.
The ideal path of the white king is to stay away from the ideal path of the black king as far as possible.

diagram 5





















green = key square
yellow = the zone where the kings could interfere.

To come any further I formulate the following hypothesis:

If the ideal path of the black king doesn't interfere with the ideal path of the white king, the black king has to leave his ideal path (= make it longer) to cause problems for the white king.
The white king can answer this by leaving his ideal path too (= make it longer), without changing the result.

I'm not going to try to prove this hypothesis. In the oncoming studies of Kp vs Kp I will see in an empyrical way if it is true and useful or not.

I hope you could stay awake :)