Topalovian weather

Chaos theory.
Fierabras said that chess is a chaotic game.
That made me think.
Say, you use a set of equations in a mathematical model to predict the temperature of the weather for the near future.
Say, the model is based on the current temperature, which you read from the thermometer as 13.345423 degrees Celsius.
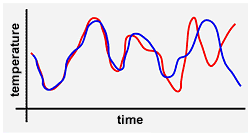
Say, you get the blue line in the graph as prediction.
Say, you do the same again with 13.345 (rounded) degrees Celsius as current temperature.
Say, you get the red line in the graph as prediction.

You see that even the slightest difference in begin temperature will lead eventually to a huge difference in prediction in the long run.
The graph can be divided in three parts.
The left part is quiet. There isn't much difference between the two predictions.
The middle part shows a difference, but is still ruled by an overal tendency.
In the right part is no correlation between the two predictions at all. All of a sudden chaos rules.
This principle was first discovered in (weather) mathematics, even with very few and simple equations, but it was discovered everywhere in nature and society too later on.

Take for instance the flow of air along a wing. At a low angle of attack (in relation to the speed) the air flows laminar. With a higher angle (and the same speed) it becomes turbulent, but still the overal tendency is to pass the wing and to generate lift. At a still higher angle of attack, all of a sudden the air flow becomes chaotic and the wing stalls.

Chaos theory in chess.
The same you will find in chess.
The slightest difference in initial state can have huge consequences in the long run. There is already one big difference in the initial state: white is to move. Even when black keeps the position quite symetrical, that will make it impossible to keep up with white.
If you take the begin position of chess, you see that the piece activity is very low. The opening is laminar, so to speak. That's why it is possible to learn openings lines. When the pieces develop, their activity increases. That's where the turbulent phase starts. By applying positional knowledge, you can have an influence on the tendency of the game. I now realize that this is what I meant by the steerability of a game.
But then, all of a sudden, when the piece activity increases beyond a certain point, the game becomes chaotic. You have to accept the positions on the board as a random given fact, and try to make the best of it. Here is where brillancy prizes are won.
With every piece that is traded, a part of the total piece activity leaves the board. In this way, when the piece activity diminishes below a certain point, the game becomes turbulent again. And with further trades, it can become laminar again.

These 3 types of flow of the game need 3 different approaches.
Different knowledge, different training methods.

Laminar stage.
The laminar stage, typical the opening end the endgame, require a very specific kind off knowledge. Knowledge that is transferable by books etc..

Turbulent stage.
For the turbulent stage, one have to study mastergames. To get a sense to steer the tendency of the game. This is the phase of subtle judgement and knowing when to break the rules. This is the "Karpovian" stage. As Karpov states, he finds a win by subtle means much more satisfactory than a win by brilliant calculation, since calculation is very error prone and risky. Since you cannot find all the lines, nor your opponent, it has an aspect of gambling for him.

Chaotic stage.
The chaotic phase is where the Kasparovs, Morozevitches and Topalovs of this world feel at home. Here take the fireworks place that is loved by the public. This is the stage that is the most difficult to learn. Here the calculation of concrete variations rules.

We are used to say that Topalov is a tactical player while Kramnik is a positional player. What we mean is that Kramnik loves the turbulent stage while Topalov loves the chaotic phase. I hypothesize that the chaotic kind of play is the strongpoint of all those child prodigies out there.

Montse said:
If you cannot win anymore from a certain strenght of player on tactics, that means also that you are not stronger in tactics but has reached the same level of strenght in your play on tactics as your opponent.

That made me think too. Am I indeed deceiving myself by thinking that I'm playing tactics at a 1900 level and positional at a 1500 level? If I look over the facts again I belief that it is indeed true that I'm a 1750 player. And a 1750 tactician. I assume that I was trying to make certain assumptions true. A bad idea. Painful to admit.

How to master chaos?
Ok, turbulent play can be mastered by studying the masters. But how to master chaotic play?
Take for instance this diagram.























White to move.
This is from one of my cc-games. The game is still running, although we are a few moves further already. SO PLEASE DON'T SEND IN ANY SUGGESTIONS ABOUT THIS POSITION!
That's not the issue I want to talk about with you. This was the position I was looking at while pondering about the above.
It is a position that I consider to be chaotic. Before I can train myself for chaotic play, I must know how to attack a position like this. And I don't know that.
I looked with Margriet for an hour or so but we couldn't find a clue.

This are a few points that arose, in random order.

• The pieces have a lot of activity. There is a lot going on for both sides.
• Positional rules/knowledge are of no use here. Concrete variations rule.
• The amount of variations caused an overload error in our short term memory. That was rather paralizing.
  
• At a certain moment we moved the pieces by hand. Although this made things easier, it did not bring us any closer to a clue. Which means that LEARNING TO VISUALIZE future positions isn't going to give us a clue either. It will make things easier, sure, but it will not give us a clue in chaotic positions.
• There is so much going on that trying to break down the position in combinational elements stranded on a memory overload error either. Even when I started to use pencil and paper.
• The sheer amount of patterns that are possible relates to the amount of patterns that I have learned as the amount of all the atoms in the universe to the amount of calories in my diet.
• The answer to the question "who is to move" makes a huge difference for the interpretation of the same geometrical situation.
• It's possible that there are no winning tactics for white (I think there are). But if there are no winning tactics around, that would be a complicating factor.
• In the end I made a move. Because I had to. It was actually a gamble. (but probably winning:)
  

Unless I learn how to crack chaotic positions like these I cannot even think about a training method. All the tactical training and the circles didn't prepare me for this position.

The romantic souls among you don't have to be anxious that I will deprive the game of it's romance with my system building efforts. That is guaranteed by the chaotic nature of the game, which can't be catched in rules.