SEE UPDATE AT THE END!!
When looking for all checks during the FAC (Find All Checks) exercise, it can be quite annoying when you have to find 8 checks, and you can only find 7 of them. Your average starts to nosedive, while your frustration hits the ceiling.
The rook, bishop and knight are easy to check. They each can give check in maximum two different ways.
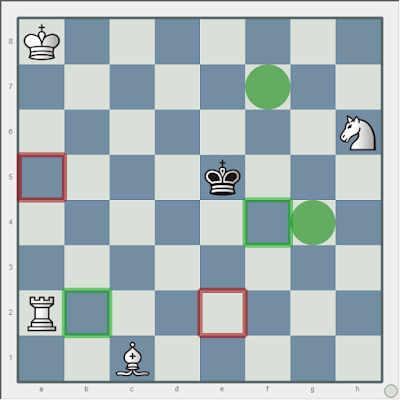 |
| White to give check |
The problem piece here is the queen, which can give check in 9 different ways, at maximum. That is because the queen can move like a rook or bishop, and can give check like a rook or bishop, in all combinations. It is easy to overlook a check, especially when the board is crammed with pieces, the checks are far apart, and/or you have to take a black piece that is heavily protected. Here is a system you might try to adopt.
By dividing the 9 possible checks in 3 sets of 3 checks, it all becomes more manageable.
When the queen and the king are on adjacent files, there are 3 squares next to the king, where the queen can give check. Imagine that the king is on d7, while the queen is on e1, then there are still 3 squares
next to the king where the queen can check. I call this set of 3 checks "queen moves like a rook"
 |
| Queen moves like a rook |
The next set of 3 I call ""Queen gives check like a rook". Again it is easy to see that if the king is on d8, and the queen is on e2, that there are 3 squares
next to the queen where white can give check as if it were a rook.
 |
| Queen gives check like a rook |
The last set of 3 checks I call the "left overs"". Two of them are on the same row as the king, while one is on a diagonal where the king is standing on.
 |
| Left overs |
When the queen and the black king are further apart, the same constellation simply stretches
 |
| Stretching |
 | |
| And even more stretching |
Of course these positions can rotate or be mirrored, and some of the checking squares can fall outside the board, but the idea remains the same. Can you still not find the last final checks, look for pawn moves. Especially the take of a piece and/or promotion can be easy overlooked. I hope it helps.
UPDATE
Here I found 12 checks. So matters are a bit more complicated. Well, it was worth a try :D
 |
| Is 12 checks the maximum? |
The black king is standing on a row, a file and two diagonals = 4 lines. The queen can give check at each line 3x at maximum. This totals to 4 x 3 = 12 checks max.
This means that the next diagram is more appropriate:
 |
| 3 checks per line max. |








See the update at the end of the post.
ReplyDeleteAfter plateauing at FAC for a few days at 12 C/Min, I went from 12 to 15 checks per minute. That means that I need 4 seconds per check in stead of 5 seconds.
At the same time I improved with M1-h. After plateauing for a week at 4 mates/min, I improved last week to 6 mates per minute. I need now 10 seconds per mate in stead of 15 seconds, which is a considerable improvement.
So it seems that improving a subtask leads to improving the main task indeed.
Thanks a lot for this article! Would you like to write another one related to check with the other pieces (Knight, King and pawn) and the one related to discovered check? I love this post and I am looking forward to next ones!
DeleteI will try to use this knowledge and see if it helps in my case.
Be careful as the improvement may be just a temporary state (not caused by the training). However if it is constant state and it is not a "standard noise" - you can really call it a progress.
To improve from 4 /min to 5 /min is already quite a positive result :) But to make M1 itself improvable ( just by solving M1 problems in the wild man mode ) it will be estimatingly necessary to improve to a much higher speed.
DeleteHere's my approach to FAC: ALL pieces have at MOST two checks (rooks, bishops, and knights) except the queen who has at most TWELVE.
ReplyDeleteUnless your R/B is blocked (setting up a pin, capture-check, or discovery), always find the TWO squares your R/B/N go to, sometimes one square might be off the board -- there are unique shapes created, which are kind of fun based on four points: the king, your piece, and the location of the two checking squares. The rook's shape is a rectangle, the bishop's shape is like a diamond, and the knight's is a funky (for lack of a better word) diamond.
The queen can deliver THREE checks along each rank, file, diagonal connected to the king. There is ONE rank, ONE file, and TWO diagonals, for a total of FOUR lines (1 + 1 + 2). That means a total possible 12 checks.
IF the queen is on the SAME color as the king, he will have all THREE on BOTH DIAGONALS, and all THREE on both rank/file. If the queen is on the OPPOSITE color, the queen will only have TWO on BOTH DIAGONALS, but still all THREE on the rank/file. Some squares will be off of the board.
Here's a post I did on this a while ago:
Deletehttp://ultimaterank.blogspot.com/2014/10/counting-checks-and-calculating-replies.html
Interesting!
ReplyDeleteThat makes several different kinds of "counting" which are useful in chess as shortcuts and pointers to possibilities:
(1) Counting the material exchanged (material count) during or at the end of an exchange sequence. Obviously, the sequence of exchanges must be taken into consideration.
(2) Counting the number of squares to Pawn promotion (the "rule of the square").
(3) Counting attacks vice restrictions vice blocks vice defenders. (Each piece gets a value of 0 or 1 on any specific square for a specific "role", without regard to material value).
(4) Counting the relative number of pieces in a particular area of the board for both sides. Essentially, this is the "three piece" rule. Using the Lord of the Rings as a mnemonic analogy: One Piece to rule them all, One Piece to find them, One Piece to bring them all, and in a checkmate bind them.
(5) Counting the number of possible checks to the King (FAC). I know this is a training subtask in and of itself, but it can prove to be very useful when trying to decide on a kamakaze attack against the opponent's King.
Off topic but related:
To Temposchlucker et all who mentioned it: Thanks for pointing out Lucas Chess. I finally downloaded it. WOW! There are a lot of very useful training tools in that toolbox!
To Aox: Thanks for creating your training tools AND for allowing unfettered access to them after closing your blog.
To Dan: I have visited your site several times without commenting, more for lack of time than any other reason. I am impressed with the depth and the thoroughness of your investigations!
To all bloggers and commentators: THANK YOU for the many ideas you have freely shared!