The ultimate algorithm of mobility
Blue Devil Knight addresses a very interesting question in his post.
How do you correctly quantify piece mobility?
Usually the value of a piece is expressed in units of 1 pawn.
Q = 9
R = 5
B = 3
N = 3
p = 1
These are STATIC values.
It can happen during a whole game that your rook stands on a1 without moving.
Sometimes it even doesn't make a difference if your rook was placed next to the board in stead of on the board.
In such cases the DYNAMIC value of the rook is 0 (zero).
In other situations the rook can be so active that it is worth a queen.
So the static value of a rook is representing the AVERAGE dynamic value of the rook.
Because we have no good algorithm to express the dynamic value of a rook, the use of the static value has become very popular.
Have a look at the diagram below.
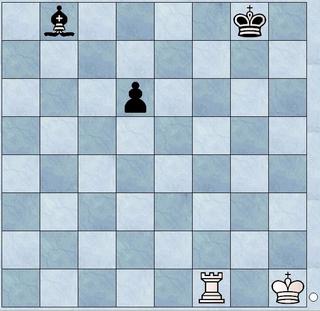
White to move.
The space of the black bishop is severely limited by its own pawn.
The space of the black king is limited by the rim of the board.
White can make use of this by playing Rc1, threatening to conquer the bishop.
If both players occupy about the same space, usually every threat can be met by a defence.
But if one of the players occupies very little space, the attacking side can change from threat to threat, and the opponent comes in trouble because he has a lack of space to move his pieces to defend against all threats.
This is a statistical matter. The CHANCE that you can do something harmful which your opponent cannot prevent increases with you having more space and he less.
All positional play is based on the principle to limit the space of your opponent and to increase your own space. Thus increasing your chances.
The ultimate goal is to take all space away from the enemy king and to conquer him.
Another important aspect to space is the element of time (begins to look like an essay of Einstein).
Have a look below.
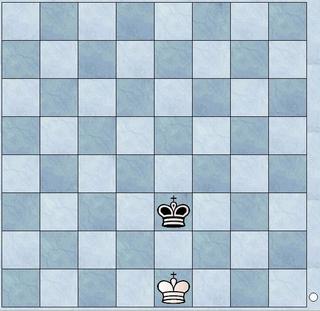
White to move.
Geometrically spoken white has almost the whole board to walk to.
But since black is to move after white, he can limit the space of the white king to the first rank.
The temporary and dynamic fence that the black king carries with him makes it difficult to find a correct algorithm to express mobility. If black is to move first, the situation is totally different.
I'm sure a correct algorithm of mobility would be a major step in solving the riddle of chess.
But untill that time we have to work with parts of the algorithm and with averages of dynamic values.
Color complexes, opposition, improve the position of your worst placed piece etc. are all parts of this same ultimate algorithm of mobility. Often these parts are simplified for convenience and easy use.
How do you correctly quantify piece mobility?
Usually the value of a piece is expressed in units of 1 pawn.
Q = 9
R = 5
B = 3
N = 3
p = 1
These are STATIC values.
It can happen during a whole game that your rook stands on a1 without moving.
Sometimes it even doesn't make a difference if your rook was placed next to the board in stead of on the board.
In such cases the DYNAMIC value of the rook is 0 (zero).
In other situations the rook can be so active that it is worth a queen.
So the static value of a rook is representing the AVERAGE dynamic value of the rook.
Because we have no good algorithm to express the dynamic value of a rook, the use of the static value has become very popular.
Have a look at the diagram below.

White to move.
The space of the black bishop is severely limited by its own pawn.
The space of the black king is limited by the rim of the board.
White can make use of this by playing Rc1, threatening to conquer the bishop.
If both players occupy about the same space, usually every threat can be met by a defence.
But if one of the players occupies very little space, the attacking side can change from threat to threat, and the opponent comes in trouble because he has a lack of space to move his pieces to defend against all threats.
This is a statistical matter. The CHANCE that you can do something harmful which your opponent cannot prevent increases with you having more space and he less.
All positional play is based on the principle to limit the space of your opponent and to increase your own space. Thus increasing your chances.
The ultimate goal is to take all space away from the enemy king and to conquer him.
Another important aspect to space is the element of time (begins to look like an essay of Einstein).
Have a look below.

White to move.
Geometrically spoken white has almost the whole board to walk to.
But since black is to move after white, he can limit the space of the white king to the first rank.
The temporary and dynamic fence that the black king carries with him makes it difficult to find a correct algorithm to express mobility. If black is to move first, the situation is totally different.
I'm sure a correct algorithm of mobility would be a major step in solving the riddle of chess.
But untill that time we have to work with parts of the algorithm and with averages of dynamic values.
Color complexes, opposition, improve the position of your worst placed piece etc. are all parts of this same ultimate algorithm of mobility. Often these parts are simplified for convenience and easy use.
To my knowledge the exact static values of pieces are:
ReplyDeleteQ = 9.75
R = 5
B = N = 3.25
Interesting post, I used to think about it earlier and came to the conclusion that it is much too complicated to evaluate the exact (dynamic) value of each and every piece, which is subject to change with every move. And please do not forget the pawns, their value is never exactly 1 pawn unit. So my solution would be something like first count static values, then add bonus and discount malus for each piece with strong/weak position. And do not forget that such counting is limited to non-tactic, quiet positions.
How calibrate bonus and malus? I think a good idea is to look at classic gambits such as Evans or Morra. The bonus of white piece activity roughly must equal a pawn, because these gambits are sound.
"If both players occupy about the same space, usually every threat can be met by a defence.
ReplyDeleteBut if one of the players occupies very little space, the attacking side can change from threat to threat, and the opponent comes in trouble because he has a lack of space to move his pieces to defend against all threats."
I think this is generally true, but not in all cases. In some cramped positions, there is a certain amount of latent dynamism that the cramped position holds. In my last OTB game, my opp had a definite space advantage AND the initiative. However, my position proved to be a tough nut to crack. True, I had to defend accurately, but once his attack was stopped, the tables were turned.
Dan Heisman also lists the values the same as what Mouse listed and as Mouse noted, these are approximations based on general factors - obviously a super Knight is worth more than a bad Bishop.
ReplyDeleteIt's important to make the distinction because too many counting errors are made by amateurs - if you understand the difference it can change way you approach the game.
One thing Mouse left out was that the Bishop pair is worth 0.5 as well.
Being down 1 pawn is like being down 2 touchdowns in an NFL qrjbgame.
CD,
ReplyDeleteI know what you mean. There seems to be a critical value of space. Good defenders can do amazing things in little space. But a little less space and their rampart collapses.
The term "space" is normally used in a rather vague way. I'm trying to point out in what direction you have to look for a more mathematical approach. It is easy to imagine a black knight in diagram 1 which has all the space in the world. So space is related to individual pieces.
J'adoube,
ReplyDeleteI know there are different schools on the subject of valueing pieces. For me a bishop is more worth than a horsey.
I just wanted to make the point that the use of static values is always inexact. The only reason to use static values is the incapability of our mind to use dynamic values.
NFL qrjbgame is way beyond my dictionary. North Floridan Quick Rugby Jockey Ballgame?
I believe that a touchdown is a term from one of those weird sports only played in America?.
Oops Tempo, never call a Knight a horsey! It will take its revenge and fork you! I also value Bishops higher most time, but I think it is a bad habit, and I can show you a lot of games I lost just for this reason.
ReplyDeleteMouse, I can't hardly take the comment serious from people who call their horsey "(jolly) jumper":)
ReplyDeleteTempo
ReplyDeleteIt was a typo. I meant NFL = National Football League, but you already knew that from the use of the term touchdown, didn't you. . .
By the way, last time I checked, the NFL had teams playing all over Europe and were quite popular. [grin]
BTW, does your horsey ever get thirsty for a drinkey? Does him wittle self need a blankey to keep comfy?
lol. . .anyway, I'd agree that assigning value during the game is inexact. Even computers have trouble doing this as the algorithms are based on our subjective assessment.
I a working on a new algorithmic approach to chess play. It involves seeing the board and pieces not as a combatative contest, but as a network requiring the reduction of white noise and interference. I'll be posting on it soon. . .
Tempo, those diagrams are absolutely gorgeous. What did you use to put them together?
ReplyDeleteMT, I use Arena (freeware).
ReplyDeletehttp://www.playwitharena.com/
The nice thing is that you can use the images of the squares in Babaschess too.
J'adoube, I'm very curious at your algorithm. BTW, I found that there are indeed 1200 football players in the Netherlands (against 1.2 million soccerplayers). The town where I reside happens even to be the dutch champion! My association with a touchdown lies between what twisters do ,wrestling and rugby. NFL stands for dutch florin (Nederlandse Florijn).
ReplyDeleteAn interesting discussion of space and material power. I wonder how Fritz uses this in its evaluation profile.
ReplyDelete>>"The CHANCE that you can do something harmful which your opponent cannot prevent increases with you having more space and he less."
ReplyDeleteI like this point. You could even argue it stronger if all pieces were traded leaving a won King and pawn endgame for the side with more space.
Here's a link for more detailed material valuation:
http://mywebpages.comcast.net/danheisman/Articles/evaluation_of_material_imbalance.htm
link for material valuation
ReplyDeleteDoesn't it matter on what squares you control, and how much force you have of those squares. Sometimes it all depends on just a few squares, so controlling other insignificant squares won't do much.
ReplyDeleteI kind of disagree of thinking of chess and positional play as an algorithm (for humans XD).
I did some research, and found a from a man that did extensive research on this whole "dynamic vs. static" issue. I agree, it is tough, and it's an age old issue, but here's his results summed up:
ReplyDelete==========
Pawn - 100
Bishop - 325
If you have both bishops - 50
Knight - 325
(+6 for each Pawn > 5 on your side
-6 for each Pawn < 5.)
Rook - 500
(+12 for each Pawn < 5 on your side
-12 for each Pawn > 5.)
Queen - 975
==========
You many notice the numbers are large, this is simply because they are meant to be dealt with mostly in programming, where integers cannot be decimals. Just divide them by 100 to get the numbers you know =P
BTW, here's the site:
Material
While it doesn't completely solve the issue of mobility, it does help. I haven't quite seen the results in action, but I'm working on a search program, and I hope to see the results in action with success.
In the mean time, good luck to you all!
oops... i just now saw that other people put up this link...
ReplyDeleteheh heh...
Well, its a good one -_-'
Anyway, now people can see the summary without going to the link.
oops... i just now saw that other people put up this link...
ReplyDeleteheh heh...
Well, its a good one -_-'
Anyway, now people can see the summary without going to the link.